Using evidence for impact in 2022 – mathematics in upper…

Introduction to the ‘evidence for impact’ blog series

With the new year well underway, schools and early learning settings across Australia are grappling with the past and present impacts of the pandemic, and now, also impacts of the floods in some parts of the East Coast. This challenging context provides an opportunity for instructional leaders to use a strong evidence base to focus upon targeted and manageable actions that support learning and wellbeing.

The impacts of the pandemic (and other disruptions such as floods) on children and young people can be highly variable, with significant differences to be expected across contexts, cohorts and circumstances. Furthermore, there is ongoing potential for additional disruption of learning and development due to isolation requirements for both educators and children who develop Covid-19 or are close contacts of those who do.

There may be impact on student achievement in mathematics, particularly for students from disadvantaged backgrounds, as the result of disruptions to onsite schooling. This blog (the second in the series) looks at what the research evidence says on mathematics instruction and identifies evidence-informed actions related to one focus area that can be addressed to improve outcomes.

What does the research say about improving problem solving in mathematics?

The Guidance Report on improving mathematics in upper primary and lower secondary has eight key recommendations, including guidance on using assessment, using manipulatives and representations, and developing mathematical knowledge. It provides a resource for planning and implementing strategies to support leaders’ decision making to bring about improvement in mathematics outcomes over the longer term. We encourage you to review all the recommendations and use the accompanying self-assessment guide to reflect on which areas of improving mathematics are most relevant for your context.

In this blog we focus on the recommendation to teach strategies for solving problems and how it can be used to make an impact now. It is particularly useful for any instructional leaders who have used school data to identify that problem solving is a challenge for their students.

A problem-solving strategy is a general approach to solving a problem, whereas an algorithm is an established series of steps executed to carry out a particular procedure. Problem solving requires greater flexibility in approach and can help students make sense of unfamiliar situations.

What is most effective in helping students develop problem solving skills in mathematics? A systematic review by the US What Works Clearinghouse indicates that evidence is strongest in support of the use of visual representations and worked examples, as well as encouraging students to monitor and reflect on the problem‐solving process.

Worked examples

The use of worked examples enables students to focus on reasoning and strategies. Dedicating classroom time to explore well-structured worked examples can also provide opportunities to identify and address possible misconceptions, and to scaffold students’ ability to work independently in mathematics. Teachers can use worked examples to model their thinking out loud, which helps to build students’ metacognitive abilities.

Visual representations

Visual representations can provide insight into the structure of a problem and its mathematical formulation. Encouraging students to make use of appropriate diagrams and representations provides them with tools they can use to access and process the information provided so that they can make a start on solving a problem.

Monitoring and reflecting on the problem-solving process

Problem solving is a process. Supporting students to see it as such can enable them to access more effective strategies and can help students overcome fears of failure or resistance to giving it a go.

While working on a problem, encourage students to ask questions, and to communicate their thinking verbally and in writing to both teachers and other students.

The following diagram, adapted from E4L’s partners in the UK at the Education Endowment Foundation, provides some useful prompts that can assist students in planning, monitoring and reflecting as they progress through the process of solving a problem. E4L’s Guidance Report Metacognition and self‐regulated learning provides further recommendations on supporting students to monitor their own learning.

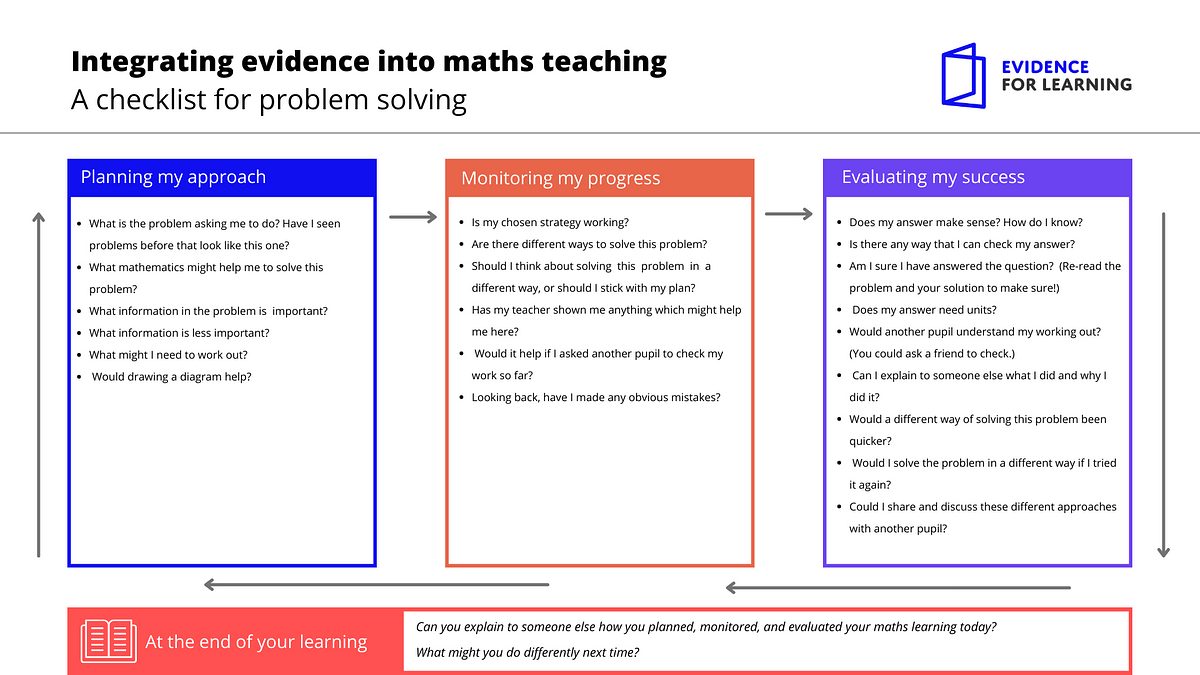
Integrating evidence into maths teaching A checklist for problem solving 1 — This diagram is adapted from E4L’s partners in the UK at the Education Endowment Foundation.

Putting problem-solving into action

Michael Rosenbrock, Assistant Principal of Wodonga Senior Secondary College reflects on problem-solving in the classroom:

The ability to solve mathematical problems is a fundamental part of a student’s mathematical toolkit and is critical to the successful application of mathematical knowledge, not only in high stakes assessment, but also in real life. In teaching a maths or physics class I dedicate class time to building students problem-solving capacity. First and foremost, I do this by always modelling my own thinking journey in solving any problem or worked example. Secondly, I take every opportunity to provide students with a range of tools, such as visual representations, and ensure they have multiple opportunities to apply them. To be effective, this must happen within a supportive classroom culture that is open to making mistakes and values the journey – and that starts with me! As an instructional leader it is critical that I support mathematics teachers to focus on problem solving. Part of this is ensuring that they have a clear understanding of: how problem solving differs from applying algorithms; and what strategies are most effective in supporting students to solve problems. It is also critical to ensure teachers have access to any resources they need to support this – in particular, making time within planning and the classroom for this vital work.

Considerations for leaders

Is problem solving a particular challenge in mathematics in your school, especially after any extended periods of remote learning? You may wish to review your student data and use E4L’s reflection tool to assist your assessment (see page 3 of E4L’s Self-Assessment Guide).
Problem solving can be confused with applying algorithms. Algorithms are established procedures to follow whereas problem solving skills can deal with unfamiliar scenarios. Is there a shared understanding amongst teachers of what is meant by problem-solving? If not, what opportunities could you use to unpack this with teachers?
Some problem-solving strategies are more effective than others. How can you best support teachers to engage with strategies such as worked examples and visual representations?
Problem solving is inherently linked to developing metacognitive skills. Are there opportunities to link problem solving approaches in mathematics to metacognitive skills and processes developed in other content areas?
Developing problem solving capabilities requires an investment of preparation time and class time. Are teachers clear that leadership values this work and that it has a strong impact on student outcomes? Are there any barriers to this in your setting that you can address?

Key takeaways

Supporting students to develop problem solving skills is an important part of mathematics instruction and one that many students might find challenging, particularly after extended periods of remote learning. Proven problem solving strategies are straightforward to implement and can be readily integrated into classroom practice.To be successful, leadership must ensure time is available to prioritise the teaching and learning of problem solving.

Evidence for Learning: Using evidence for impact in 2022 – mathematics in upper primary and secondary schools