Introduction
We as humans, tend to focus on negative news. In fact, there are whole industries that are geared around bad news (Pinker, 2018). In evolutionary terms this is because we needed to pay attention to the bad news e.g. where we had a high likelihood of being in danger (Simler & Hanson, 2018). Risk of harm was more important than possible benefit. We still hang onto this trait even though now it is not so useful for us (Simler & Hanson, 2018). Considering this we are going to address key arguments raised against meta-analysis, in the hope that by doing so we can let go of the ‘bad news’ and embrace the magic of the effect size.
Where were you when you first calculated an effect size?
A focus on the negative can be heard in conversations that start with, ‘do you remember where you were when [insert famous person’s name here] died’ or ‘do you remember where you were when [insert a tragic event] occurred.’
We want to turn this idea upside down by asking you, ‘do you remember where you were when you calculated your first effect size?’
Dr Tanya Vaughan remembers her calculation quite clearly; she was just about to submit an Evaluation report to The Song Room for an impact study she had led in 12 schools in South Western Sydney. A bit of background to this story is Brian Caldwell, who Tanya was fortunate to be working with, handed her a book that was to change her statistical life. It was Visible Learning by John Hattie (Hattie, 2009). In reading this book Tanya could see the value of using a measurement that allowed a universal language for educators, a bit like the creation of the language of chemistry in the periodical table. It meant that we could compare between different studies across the world. So, Tanya decided that she would calculate effect sizes for the data that she had collected from the schools involved in the project. The first one Tanya calculated produced an effect size of 0.77, she was excited, it met the threshold of over 0.4 to be considered as a real life impact. In the end Tanya and her colleagues presented their results at Parliament House, Canberra (Vaughan, Harris, & Caldwell, 2011) and wrote a book for the international publisher Routledge (Caldwell & Vaughan, 2012).
Why are effect sizes magical?
They are magical as they enable communication between researchers around the world.
Without effect sizes, an impact on ATAR scores in Australia would be incomparable with an impact on a GCSE score in England.
Imagine a mathematical tool that lets everyone talk in the same language. Like the periodic table for writing chemical equations, it is globally known that Na is Sodium and NaCl is table salt. Gene Glass (the creator of the effect size) had come up with a useful way forward for statistics. Educational research could now be brought together.
Crucially, for the Teaching & Learning Toolkit, effect sizes also allow individual results from different tests to be synthesised. By looking at effect sizes in combination, we can begin to build up a more rigorous evidence base for education interventions.
Although, synthesising effect sizes is not without criticism. In working with practitioners across Australia, Evidence for Learning team members are often asked to respond to the arguments against meta and meta-meta analysis. Recently Tanya was part of an Educators Reading Room Podcast (ERRR) where Professor John Hattie addresses these criticisms in greater detail (released 1 June, http://www.ollielovell.com/errr/johnhattie/) than we can here, in response to a previous podcast by Professor Adrian Simpson (Lovell, 2018).
For the purposes of this blog we will be looking at four main arguments against meta-analysis (Simpson, 2017) and what they mean for educators. The four main arguments raised are 1) comparison groups, 2) range restriction, 3) measure design and 4) that meta-analysis is a category error.
Comparison groups
The key argument here is that you can’t compare studies that have different comparison groups as the effect size will change dependent on the comparison group. Yes, it is true that if we change the comparison group the effect size will change.
An effect size is calculated by taking the mean of the ‘treatment’ group and subtracting it from the mean of those in the control/comparison group, and then dividing by the spread (the pooled standard deviation) as seen in figure 1.
So, if you change the control group then you change the overall effect size.
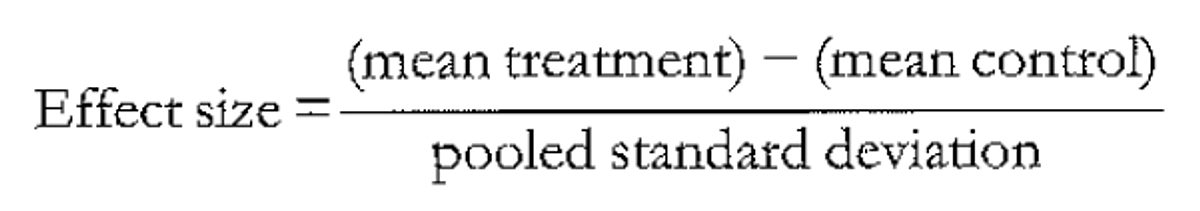
Figure 1: The equation for the calculation of an effect size
For the Teaching & Learning Toolkit (the Toolkit) (Education Endowment Foundation, 2018) we have worked to overcome this by choosing studies with robust and appropriate comparison groups and using the padlock evidence security rating (Table 1). If a study in the Toolkit involves a less robust comparison this is given a lower padlock rating to let the users know that the evidence is not as trustworthy as other approaches. In building new evidence through (Evidence for Learning, 2018), four trials have been commissioned by Evidence for Learning (a majority of them being randomised controlled trials) to identify programs and approaches that work best at raising achievement and sharing this with educators in the most accessible way possible. Within the randomised controlled trials, control groups allows us to compare and see what happens when an intervention is introduced in order to form an effective observation.
Table 1: Evidence security ratings
Through the Learning Impact Fund, Evidence for Learning commissions and funds independent evaluations that use robust control groups through randomised controlled methodology. Randomised controlled methodology has the benefits of:
- Eliminating selection bias and can generate a causal conclusion;
- Avoiding potentially misleading results from non-experimental work which has inadequately controlled for selection bias;
- Providing a quick and digestible conclusion of program effectiveness that avoid lengthy caveats; and
- Results can be incorporated for future meta-analysis (Hutchison & Styles, 2010)
The results of the first Learning Impact Fund trials are targeted for release this year (Evidence for Learning, 2018). It is an evaluation of a Professional Learning Program for Mathematics Teachers called Thinking Maths with the Australian Council for Educational Research as the Independent Evaluator. Two other randomised controlled trials are currenting being undertaken with a phonics based program for early readers who are struggling (MiniLit) and a program called QuickSmart Numeracy that is focused on increasing mathematics automaticity in primary school learners. Evidence generated from these trials will be able to be added to the Toolkit as they meet the robust requirements. A pilot evaluation on a program that supports students’ resilience and wellbeing called Resilient Families is also being conducted to understand feasibility of the program before committing to a randomised controlled trial.
Range restriction
The main argument about range restriction is that by limiting the variety in the group studied you can increase the effect size. If we use more homogeneous groups (e.g. narrower sampling with a group – with less variance) we reduce spread therefore reduce denominator (the pooled standard deviation) and increase effect size. Range restriction doesn’t increase the difference between the treatment and control group, but by reducing what we divide that difference by we increase the effect size. This means that range restriction impacts effect size by reducing the within-group variance and thus reduces the spread in the calculation of an effect size. That is, it reduces the denominator in the effect size calculation thus increasing the overall effect size.
Range restriction is a problem in some meta-analyses and at least partly explains why targeted interventions tend to have higher effect sizes. Narrower sampling criteria tend to reduce the standard deviation (spread). This directly affects the effect size as the standard deviation is used as the divisor – the smaller the spread, the larger the effect size. So catch-up approaches might be expected to have larger effects because they include a restricted range of the population.
Measure design
The key argument about measure design is that the choice of the measurement of the impact can increase or decrease effect size. If it’s close to the change made it will increase, if it’s a standardised test it will most probably decrease. The measure we use to determine the impact of an approach can influence the effect size. There is an increased chance of finding a difference if a test is closely tied to the change in approach. We like to think of this as proximal (being closer to the activity) and distal (being further away from or removed) measures.
We always try to use outcomes in the Toolkit which predict wider educational success (such as reading comprehension or a standardised test of mathematics).
This is a tough test for an approach, where you might first want to know does it work as intended (e.g. improving phonics to increase letter and word recognition or teaching a specific aspect of mathematics which improves number fact recall). A proximal measure, closely aligned to the approach will tend to show higher effects, such as knowledge of letter sounds as opposed to reading comprehension which is more distal, but a better overall predictor of educational success. Another example of a proximal measure might be a number test related to what was taught, as opposed to a standardised test of mathematics.
In terms of the Toolkit there are two things to consider:
- the impact on a specific strand and
- the impact on any comparisons between strands.
Range restriction or measure design (and other factors which seem to be related to effect size, like student age or sample size) may well be influencing the overall estimate. Though this may be misleading in terms of the typical effect, the estimate will apply to similar populations (e.g. teachers interested in helping struggling students or younger children) and similar outcomes (narrower areas of reading or mathematics).
The Toolkit methodology is applied consistently between strands – we cannot, for example, choose to only look at standardised tests for homework and only look at proximal measures for mastery learning.
Therefore, we think that taken all together it is still useful to use meta-analysis to help inform decisions in education both for the profession and to inform policy.
Category error
The last argument we will address here is that of category error. The argument being raised is that because effect sizes can be changed by altering the comparison groups, using range restriction and different measures they should not be combined in a meta-analysis and when they are it forms a category error. The key argument is that using meta-analysis (thus effect sizes) in education is like determining the age of a cat by measuring its weight (Lovell, 2018). We disagree with this, in meta-analysis we are measuring a range of students’ learning outcomes which are related to education.
In combining effect sizes, we are trying to collect together the best available evidence for what has been effective in changing educational outcomes. Even accepting some limitations of meta-analyses (or meta-meta) they provide a very useful introduction into a body or areas of research knowledge to give a busy practitioner a starting point or way into a complex topic.
They do not treat it like the last word on the topic but they can treat is as the first word and summary on where the weight of evidence lies.
Conclusion
That brings us back to the question, so where were you when you calculated your first effect size? Maybe your first time is still coming. Tanya was fortunate a few weeks ago to be in a room full of Monash University undergraduate and postgraduate Teacher Education Students’ helping them to calculate their first effect sizes. The room was a buzz of excitement.
Are effect sizes all we need to make decisions in education? No, they are just a useful starting point. The classroom is full of rich data, both small and big data that is helpful to the teacher to determine if their change is having the desired impact. Like John Hattie, we are passionate about schools being ‘incubators of programs, evaluators of impact and experts at interpreting the effects of teachers and teaching on all students’ (Hattie, 2015, p. 15). This is exciting and the beginning of an evidence adventure, part of which will include the magic of effect sizes both to inform decisions based in evidence and for practitioners to gather their practice-based evidence.
Authors
Dr Tanya Vaughan is an Associate Director at Evidence for Learning. She is responsible for the product development, community leadership and strategy of the Toolkit.
Jonathan Kay is Research and Publications Manager at the Education Endowment Foundation (EEF). Jonathan manages the EEF evaluation reports, and supports the development of the Toolkit.
Professor Steve Higgins is Professor of Education at Durham University. He is one of the authors of the EEF Teaching and Learning Toolkit.
References
Caldwell, B. J., & Vaughan, T. (2012). Transforming Education through The Arts. London and New York: Routledge.
Education Endowment Foundation. (2018). Evidence for Learning Teaching & Learning Toolkit: Education Endownment Foundation. Retrieved from http://evidenceforlearning.org.au/the-toolkit/
Evidence for Learning. (2018). The Learning Impact Fund. Retrieved from http://evidenceforlearning.org.au/lif/
Hattie, J. (2009). Visible Learning: A synthesis of over 800 meta-analysis relating to achievement. London: Routledge.
Hattie, J. (2015). What works best in education: The politics of collaborative expertise. Open ideas at Pearson, Pearson, London.
Hutchison, D., & Styles, B. (2010). A guide to running randomised controlled trials for educational researchers. Slough: NFER.
Lovell, O. (2018). Education Reading Room Podcast: Adrian Simpson critiquing the meta-analysis. Retrieved from http://www.ollielovell.com/errr/adriansimpson/
Pinker, S. (2018). Enlightenment Now: The Case for Reason, Science, Humanism and Progress: Penguin.
Simler, K., & Hanson, R. (2018). The Elephant in the Brain: Hidden Motives in Everyday Life. New York: Oxford University Press.
Simpson, A. (2017). The misdirection of public policy: Comparing and combining standardised effect sizes. Journal of Education Policy, 32(4), 450 – 466.
Vaughan, T., Harris, J., & Caldwell, B. J. (2011). Bridging the Gap in School Achievement through the Arts: Summary report. In. Retrieved from http://www.songroom.org.au/wp-content/uploads/2013/06/Bridging-the-Gap-in-School-Achievement-through-the-Arts.pdf
